Day 13: Compactness guarantees sequential compactness (with pictures!)

I think I’m starting to understand why I was so unchill (reliant on proofs by contradiction). It’s because Metric Spaces is violent like that.

Here, violence (contradiction) is rationalized in service of a fairly gentle (constructive) conclusion.

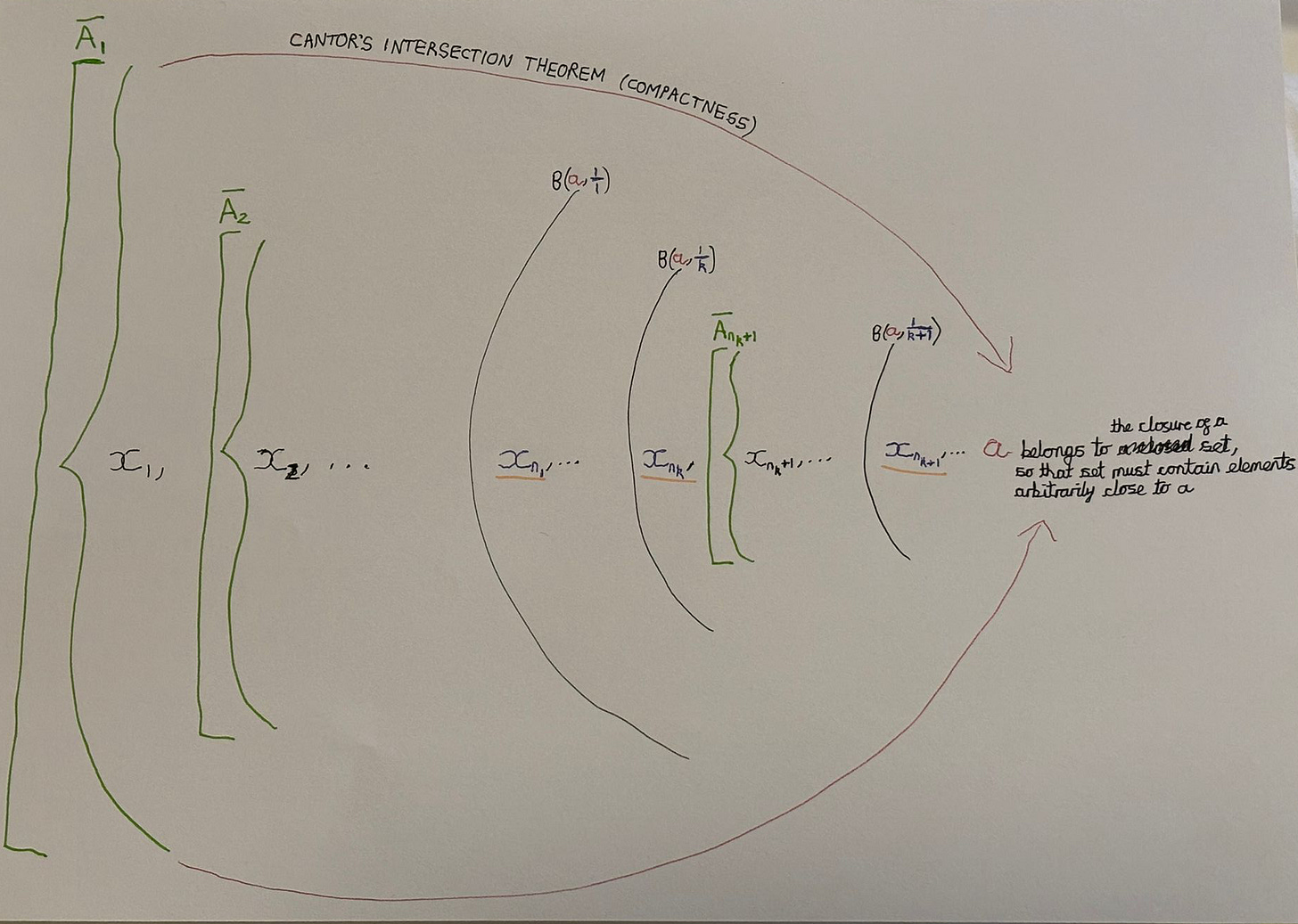
Cantor’s Intersection Theorem (Compactness)

The intersection of a nested sequence of nonempty closed sets in a compact space is nonempty

violence! (horizontal arrows / lowercase represent racking focus, vertical arrows / uppercase represent deductive ‘work’)

shout the element(s) in the intersection!

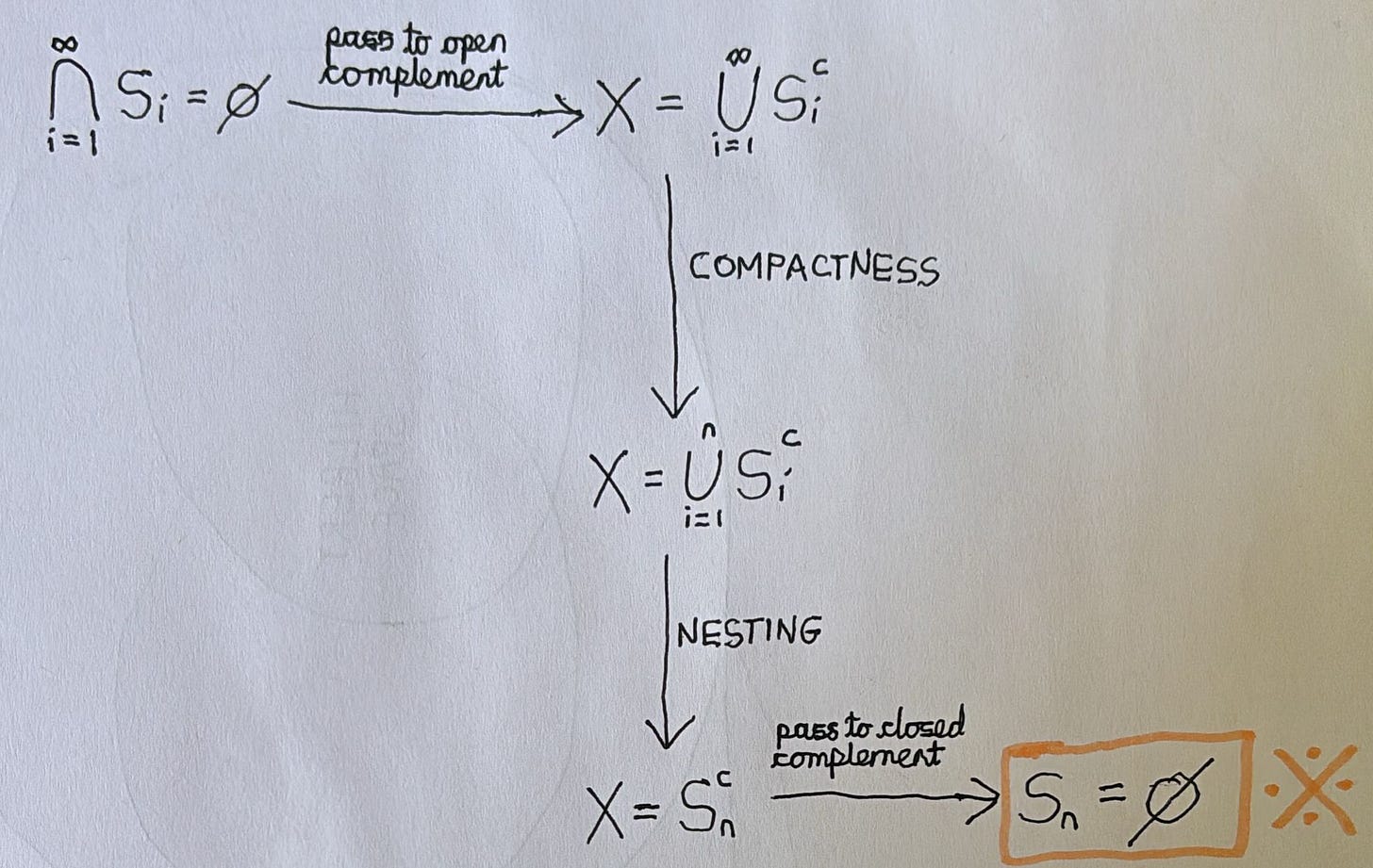
Compactness implies Sequential Compactness

‘Compactness’ used only through Cantor’s Intersection Theorem!

We’re using closed sets to guarantee the existence of elements. The nested sets guarantee the existence of a. Those same sets guarantee the existence of elements arbitrarily close to a; we construct another closed set to prove the existence of each next point in our sequence converging to a.