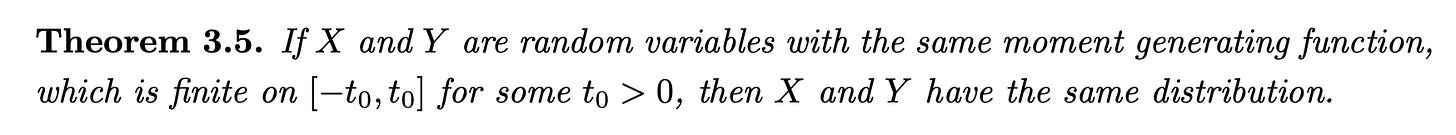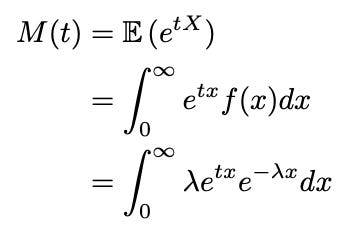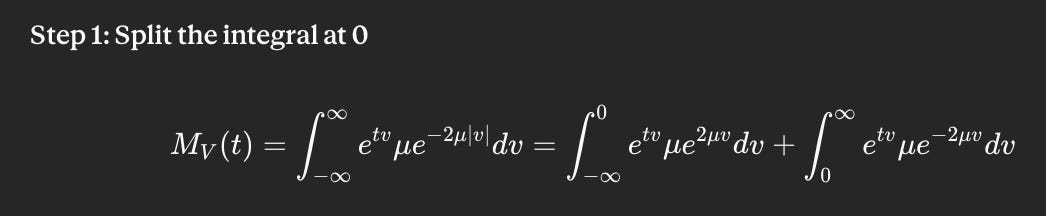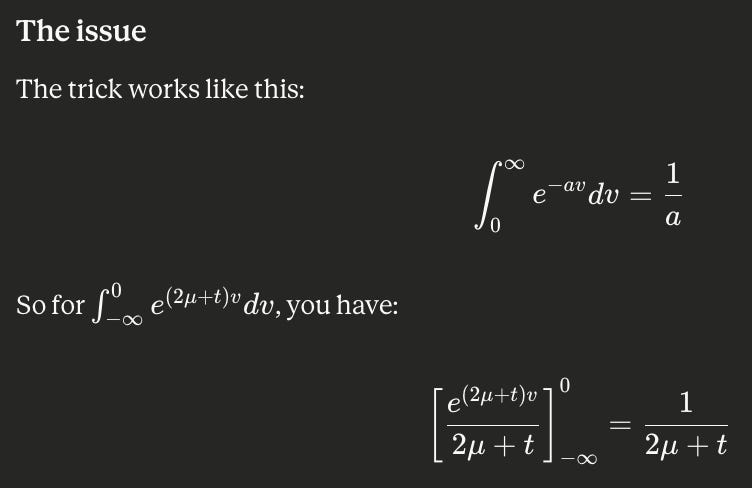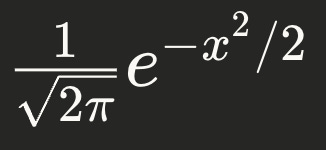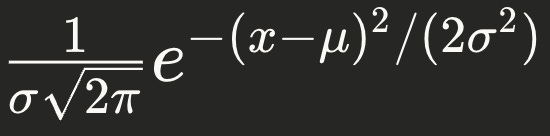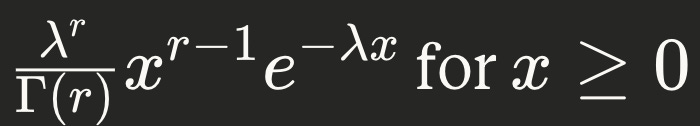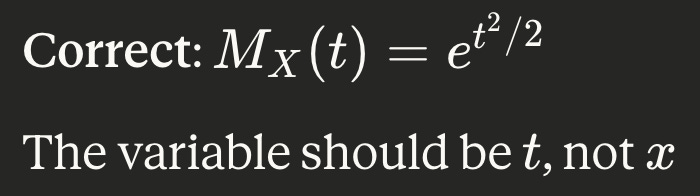Day 21: Moment Generating Functions

Great—a new mathematical object to play with!

(note the type signature: always from the reals to the non-negative reals. may or may not include infinity)

I instinctively like this because it encodes lots of information in a single mathematical object. Compresses it s.t. it can later be retrieved.

The way it does this is neat and familiar:

yields an easy quick check: MGF at 0 should always equal 1

If two distributions have the same MGF finite on some interval including 0, they must be the same distribution.

We like ‘uniqueness properties’. Recently, we’ve used the uniqueness of limits, and seen the uniqueness of a contraction’s fixed point. Uniqueness soon becomes a standard argument move.

This works because MGFs are analytic functions (have convergent power series expansions).

The next thing to appreciate is some basic integral manipulation. Yay, tsuyoku naritai when it comes to integration!

MGF of Exponential Distribution

MGF of Normal Distribution

camel principle to complete the square

The Camel Principle

I satisfied myself that I know how to find the MGF of Y = aX+b, given the MGF of X. From that, I could get the MGF of N(μ, σ²) for any μ, σ, since I know X ~ σZ + μ. I satisfied myself that the MGF of some sum is the product of those summands’ individual MGFs. From that, I could get the MGF of two normal distributions summed.

I would need to re-derive a lot of this stuff on the spot, though. I’m letting myself memorize the Normal density function :/, although this is an excellent derivation. I should probably remember some ‘endpoints’ so I have a sense of where I’m headed when deriving…

Generalized MGF Derivation Flow

Decoding Moments

Actual Applications

To be honest, the textbook always tries to use ‘real-world examples!’ like waiting for a bus, and those just don’t track my world.

Here are some examples that track my actual world:

1 is clearly broken (it depends on what the other labs do). 2 is interesting and real. Re 3, we are definitely in a critical period; we can’t draw inferences from the past several million years to tell us about these few. 4 might be more significantly more realistic than 1 to be honest 😅 — less at-scale coordination taking place. 5 is informative and kino.

GPU failure is a very sympathetic example; I’ll use that by default from now.

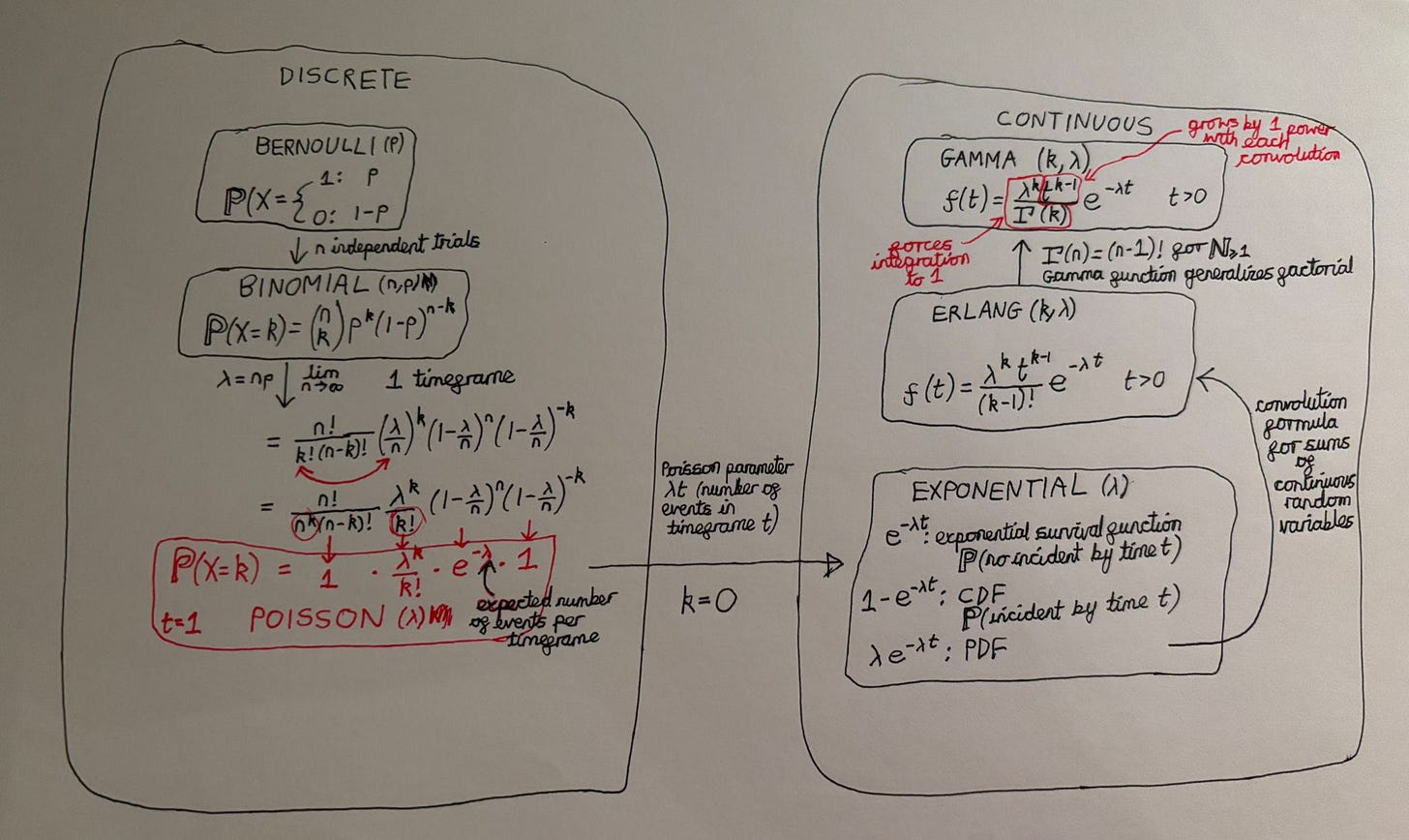
Gamma Function…

thank you opus! gpu failure is doing the heavy lifting here

First we need to understand what’s going on with the Gamma function.

Summing random variables convolves their densities! Multiplies their MGFs. Convolution in “density space” becomes multiplication in “MGF space.” This is the same reason Fourier transforms are useful: they turn convolutions into products.

convolution detour. this is extraordinarily cool. i knew camel principle mattered…

(See penultimate image of this post for MGF derivation)

Splitting integrals to address absolute value

To test what I’d learned, I worked through this problem.

The main takeaways stemmed from (v). I worked through this pretty effectively, but above all I should’ve split the integral:

I also tried to factor out terms from the exponent in order to get a PDF integrated over its support, which yields 1. But instead I could’ve (& should’ve) just integrated directly:

Once I got this, I got the whole problem!

Main use case of MGFs:

• We have some MGFs. We do a bunch of manipulations on them. We get out another MGF. We recognize it as the MGF of some known distribution! By uniqueness, we can identify sweet relationships between distributions this way :) If they have the same MGF, they must be the same distribution.

Things I need to be drilled on

(I’ll feed screenshots of this to Claude :))

• PDF of N(0,1)

the 2 appears three times.

• PDF of N(μ, σ²)

scale by variance in both denominators.

• PDF of Exp(λ)

i forgot the x, which is concerning.

• PDF of Gamma(r, λ)

as in Exp, i forgot the x, but also the λ^r up top. it’s a bit like Poisson

• MGF of N(0,1)

use x for PDFs and t for MGFs. it’s a bit like PDF but sign-flip and t!

• MGF of N(μ, σ²)

when i calculate the MGF of some linear transformation of a distribution, there’s a tiny risk i shove the ‘a’ in the subscript with X rather than elevating it up top in the brackets. don’t do that. i should remember to elevate it up top in the brackets

it’s good for me to write out this 2x2 table

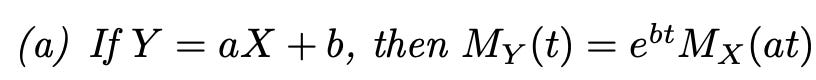
• MGF of Gamma(r, λ)

Wow! I learned how to derive MGF for Normal(μ, σ²), Gamma(r, λ), Exp(λ) (which also involved reviewing PDFs of these), + reviewed uniqueness and independence (sum variables → multiply MGFs). We don’t look at PGFs so much because that’s Prelims material.

Tomorrow’s Day 2. One down of three intense days!

Working through derivations:

• Find a bad transition probability (somewhere I frequently err)

• Hammer it out

• Repeat